F. A. Costabile, francesco.costabile@unical.it
M. Ruffolo, martina_ruffolo@libero.it
G. Tricoli, gianluca.tricoli@unical.it
“ We love Mathematics;
We love coding;
And we love the power of the two combined.”
1. Introduzione
A partire dagli anni ottanta del secolo scorso i Personal Computers cominciarono a diffondersi anche nelle scuole italiane a cominciare, naturalmente, da quelle secondarie di primo grado. In quegli anni la rete telematica non esisteva ancora, i linguaggi di programmazione presentavano una sintassi rigida con una logica che, spesso, separava l’utente terminale da un mondo che appariva complesso, esclusivo e, dunque, riservato agli addetti ai lavori. L’allora Ministero della pubblica istruzione, oggi Miur, non poteva non accogliere quella che appariva la sfida del futuro, e varò il piano nazionale di Informatica (P.N.I.) coinvolgendo i docenti di Matematica e Fisica della scuola secondaria superiore. Ci furono subito i primi entusiasti, le iniziative crescevano, ma un vero cambiamento metodologico dell’insegnamento\apprendimento della matematica non sembrò attecchire. Seguirono comunque, almeno sulla carta, altre iniziative ministeriali e non. Per un’analisi abbastanza esaustiva fino al 2013, si rinvia a [1, pp. 42-64]. Segnaliamo, in ogni caso, che con l’avvento dei CAS (Computer Algebra System) e dei DGS (Dynamic Geometric Software) l’interesse verso la programmazione da parte dei docenti di matematica, ma anche dei ministeriali, sembrò affievolirsi, quasi a scomparire, salvo rare se pure interessanti esperienze. Negli anni recentissimi tuttavia si nota una rinnovata attenzione anche, e soprattutto, a livello istituzionale per l’apprendimento della programmazione, ora più nota col nome di Coding. Infatti, grazie a spinte provenienti d’oltre Alpi e dai colossi, di turno, dell’informatica, il Miur ha avviato iniziative di incoraggiamento e diffusione di pratiche di Coding a partire dalla scuola primaria e secondaria di secondo grado. In questo articolo vogliamo riprendere il parallelismo Coding-Matematica o, come più ci piace, Programmazione-Matematica e mostrare come questo connubio si possa effettivamente realizzare con un software adeguato, ad esempio Matcos.Il resto del lavoro è cosi organizzato: nel secondo paragrafo si richiamano i caratteri essenziali del Coding; nel terzo della matematica. Nel quarto paragrafo si tenta di enucleare gli aspetti metodologici comuni alle due discipline. Nel quinto si presenta il software Matcos nelle sue linee generali. Infine nel sesto paragrafo si riportano esempi di pratica didattica in aula e si menzionano esperienze avvenute in alcune scuole della Calabria e non. Conclusioni ed auspici chiudono il lavoro.
2. Coding: significati e procedure
Coding è una parola della lingua inglese, alla quale corrisponde in lingua italiana la parola Programmazione, intesa come rivolta all’Informatica, o meglio, alle macchine computazionali di ultima generazione. In tal senso il Coding se non è sinonimo, certamente stimola e supporta il pensiero computazionale, ovvero il pensiero attivo rivolto alla soluzione di problemi di varia natura. Per la capacità di risolvere un problema pianificando una strategia, si potrebbe dire che il pensiero computazionale è un processo logico-creativo che consente di scomporre un problema complesso in diverse parti, più semplici da risolvere. Trovando la soluzione a ciascuna di esse è possibile risolvere il problema generale.
Pensare di introdurre nella pratica didattica della nostra scuola primaria e secondaria il Coding, dunque, equivale ad un approccio metodologico che mette la Programmazione al centro di un percorso formativo, dove l’apprendimento, già a partire dai primi anni di vita, percorre strade nuove ed è al centro di un progetto più ampio che abbatte le barriere dell’informatica, stimolando un approccio volto alla risoluzione dei problemi.
Inteso in questo senso, di Coding nella scuola italiana di ogni ordine e grado ce n’è stato e ce n’è veramente poco, come testimoniano alcune statistiche a cura della filiale italiana della Samsung e riportate nell’articolo di G. Mosea ([2]).
3. Matematica: significati e metodi
La matematica si esplica attraverso un linguaggio artificiale, rigoroso, astratto e con proprie regole grammaticali e sintattiche. Questa caratteristica, se da un lato ne ha determinato la sua importanza diventando il linguaggio di tutte le scienze, dall’altro pone serie difficoltà di apprendimento per i giovani allievi. Infatti sempre più spesso capita che l’essenza dei concetti matematici, ovvero le proprietà dei suoi oggetti, non traspare in tutta la sua forza ed importanza, ma resta sommersa da un apparato formale che non tutti gli studenti riescono, nell’immediato, a “graffiare” per poter “vedere ed apprezzare” il “nocciolo della sostanza”. Ne consegue spesso un parziale o superficiale apprendimento, destinato a scolorirsi sempre più col tempo. Sulla base di queste difficoltà oggettive, molti docenti si limitano ad un insegnamento puramente formale-dichiarativo, trascurando l’attività di pensiero attivo, che è uno dei paradigmi pedagogici della disciplina. Occorre, dunque, un cambiamento profondo nei metodi di insegnamento della matematica nella scuola secondaria e primaria. È necessario che lo studente diventi protagonista del suo processo di apprendimento attraverso un’attività di pensiero finalizzato. In altre parole l’allievo deve essere costruttore attivo delle proprie conoscenze, all’interno di un contesto in cui l’insegnante assume il ruolo di guida alla reinvenzione della matematica, intesa quest’ultima, come appropriazione dinamica di idee, strutture e procedimenti. In questo modo i concetti della disciplina diventano patrimonio conoscitivo, capace di sviluppare competenze di natura strategica, atte a sorreggere e orientare i processi cognitivi verso l’interiorizzazione, e l’uso consapevole delle conoscenze acquisite, atte a supportare situazioni di problem solving. Oggi, più che mai, l’attività di problem solving è di fondamentale importanza nel bagaglio formativo delle future generazioni.
4. Coding e matematica
Dai pochi concetti esposti traspare in maniera chiara che le due discipline, Programmazione e Matematica, hanno caratteristiche epistemologiche, obiettivi e metodi comuni. Ad esempio entrambe necessitano di un linguaggio artificiale, astratto, proprio e finalizzato per poter esprimere la loro funzione nei vari campi del sapere e della quotidianità. Entrambe pongono l’accento sulla necessità di un’attività di pensiero attivo, che sfoci nel problem solving, ovvero in quell’attività rivolta alla soluzione di problemi di varia natura, con un procedimento standardizzato:
- situazione problematica;
- individuazione di una strategia risolvente;
- possibile sdoppiamento in problemi di natura più semplice;
- dalla soluzione di ogni singolo problema, consegue la soluzione del problema dato.
Questo percorso si conclude con l’enunciazione dell’algoritmo risolvente, ovvero di una procedura che in un numero finito di azioni, fornisce la soluzione esatta, eccezione fatta per gli errori inevitabili, o la soluzione approssimata con indicazione dell’errore commesso. L’algoritmo risolvente per diventare operativo necessita di un’effettiva esecuzione che, oggi giorno, avviene con strumento elettronico, digitale. Tali macchine calcolatrici sono dotate di un proprio sistema operativo e di un linguaggio di codifica. Tale linguaggio è chiaramente una caratteristica fondamentale della Programmazione, che spesso ne diventa anche una difficoltà di apprendimento per i giovani allievi. Come abbiamo detto, anche la matematica è dotata di un proprio linguaggio di comunicazione. Allora se si vuole trovare un nesso comune tra le due discipline occorre costruire un linguaggio che sia compatibile con la macchina disponibile, ma che nel contempo sia il più vicino possibile al linguaggio matematico, in modo da favorire l’apprendimento. Con questo obiettivo, come diremo meglio nel prossimo paragrafo, è sorto il Progetto Matcos.
5. Il Progetto Matcos
Il Progetto Matcos, ideato e condotto ne primi anni 2000 nel C.I.R.D. (Centro Interdipartimentale per la Ricerca Didattica) [3], si basa sulle seguenti assunzioni pedagocighe-formative:
- Avviare lo studente alla programmazione, utilizzando i concetti matematici della relativa fascia d’età scolare;
- Apprendere la matematica, “pensando e facendo” con l’uso continuo e sistematico del calcolatore elettronico, quale strumento da programmare.
Con questo obiettivo non si poteva non prevedere:
- L’esistenza di un ambiente di programmazione finalizzato alla Matematica ed adeguato alle capacità logico-intellettive e linguistiche degli utenti, ovvero studenti della scuola secondaria e primaria;
- Una metodologia didattica per l’apprendimento della Matematica basata soprattutto sull’acquisizione di concetti sul problem solving, quindi sui modelli ed algoritmi.
Di fondamentale importanza è il paradigma pedagogico: CONGETTURA-VERIFICA/DIMOSTRAZIONE/CONFUTAZIONE.
Per il punto 1 è stato creato l’ambiente di programmazione denominato Matcos, che ha le seguenti specifiche:
- Nella lingua madre dello studente, in modo da non sommare alle difficoltà di apprendimento della Matematica e della Programmazione, anche quelle di natura linguistica;
- Orientato alla Matematica, nel senso che fa uso di istruzioni specifiche per taluni concetti matematici utilizzando, ove possibile, lo stesso termine matematico o sue abbreviazioni, ad esempio: punto, retta, cir. Funzione, derivata funt, ecc.;
- Esecuzione passo-passo, in modo che lo studente possa rendersi conto di ogni passo dell’algoritmo o di ciò che il computer realmente esegue;
- Modulare, ogni modulo corrispondente ad una fascia d’età, ovvero ad un preciso anno scolare; naturalmente ogni modulo include il precedente e ciò per evitare fughe in avanti.
Per quanto riguarda la metodologia didattica, ovviamente in questo contesto non possiamo fare una descrizione sistematica ed esaustiva, per cui ci dobbiamo limitare a qualche idea che traspare dagli esempi [5]..
6. Esempi
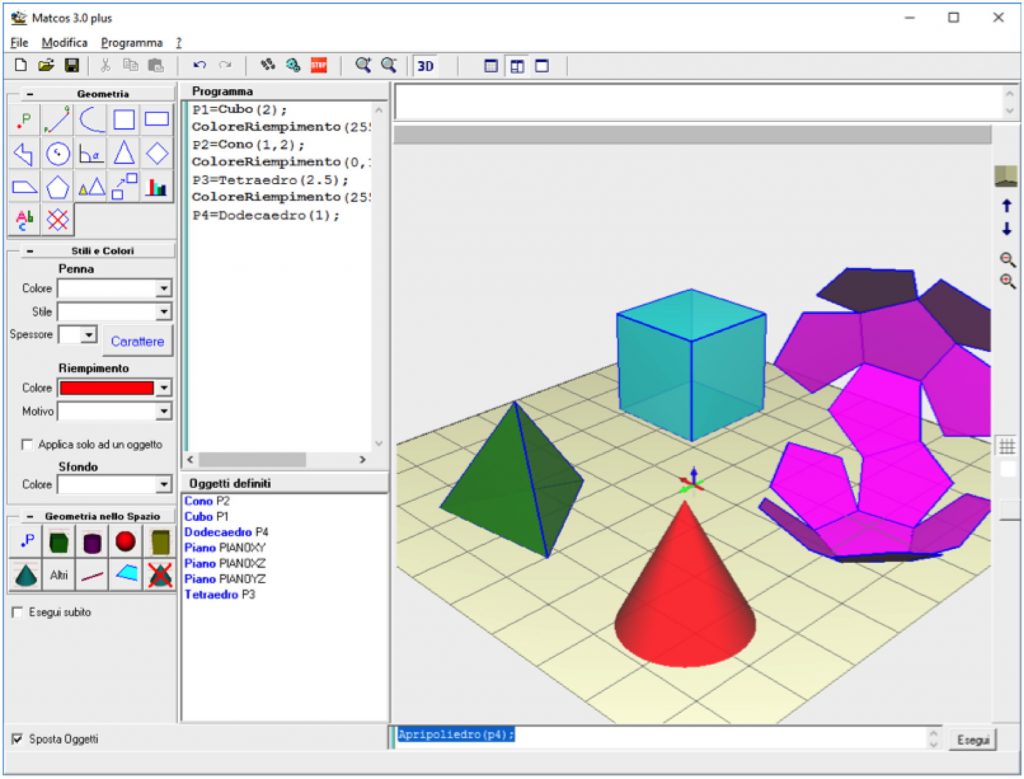
Figure nello Spazio
Il seguente programma ha lo scopo di illustrare il concetto di spazio tridimensionale e delle principali figure geometriche che si studiano nella scuola secondaria e primaria [4]. Naturalmente l’insegnante deve saper adeguare le varie istruzioni nelle diverse situazioni didattiche che creerà in aula.
P1=Cubo(2);
ColoreRiempimento(255,0,0);
P2=Cono(1,2);
ColoreRiempimento(0,128,0);
P3=Tetraedro(2.5);
ColoreRiempimento(255,0,255);
P4=Dodecaedro(1);
Apripoliedro(p4);
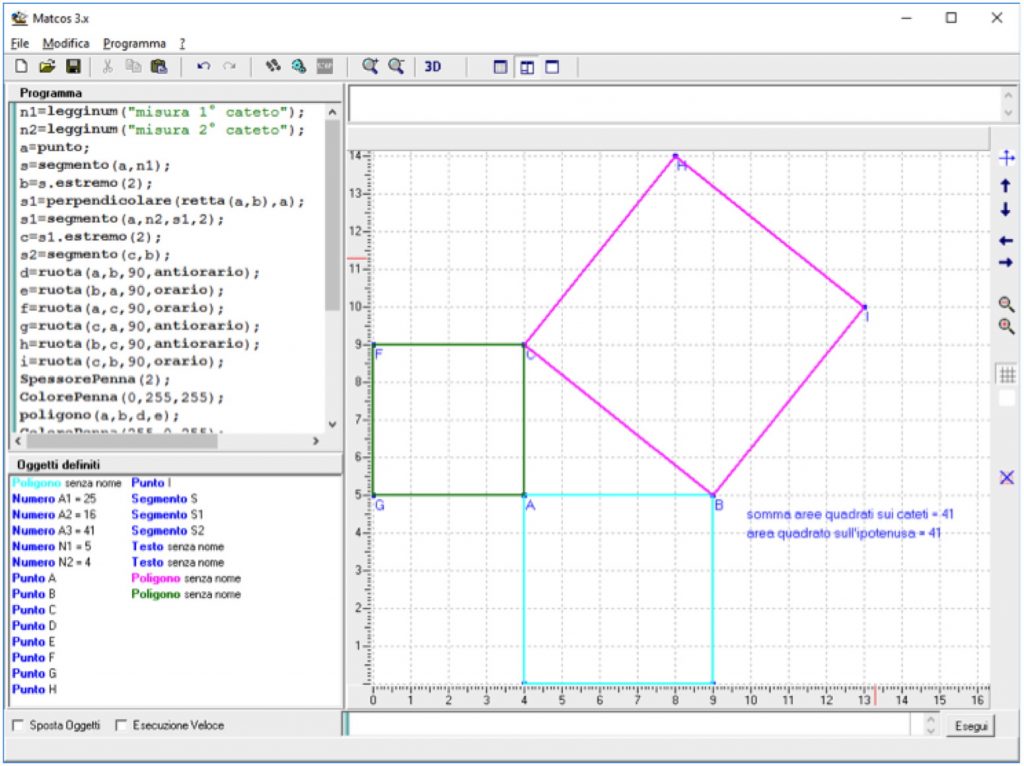
Teorema di Pitagora
Il programma utilizza semplici comandi che devono già essere patrimonio acquisito degli allievi. Illustra e verifica il contenuto del noto Teorema.
n1=legginum(“misura 1° cateto”);
n2=legginum(“misura 2° cateto”);
a=punto;
s=segmento(a,n1);
b=s.estremo(2);
s1=perpendicolare(retta(a,b),a);
s1=segmento(a,n2,s1,2);
c=s1.estremo(2);
s2=segmento(c,b);
d=ruota(a,b,90,antiorario);
e=ruota(b,a,90,orario);
f=ruota(a,c,90,orario);
g=ruota(c,a,90,antiorario);
h=ruota(b,c,90,antiorario);
i=ruota(c,b,90,orario);
SpessorePenna(2);
ColorePenna(0,255,255);
poligono(a,b,d,e);
ColorePenna(255,0,255);
poligono(b,c,h,i);
ColorePenna(0,128,0);
poligono(a,c,f,g);
a1=distanza(a,b)^2;
a2=distanza(a,c)^2;
a3=distanza(b,c)^2;
scrivi(“somma aree quadrati sui cateti = “,a1+a2);
scrivi(“area quadrato sull’ipotenusa = “,a3);
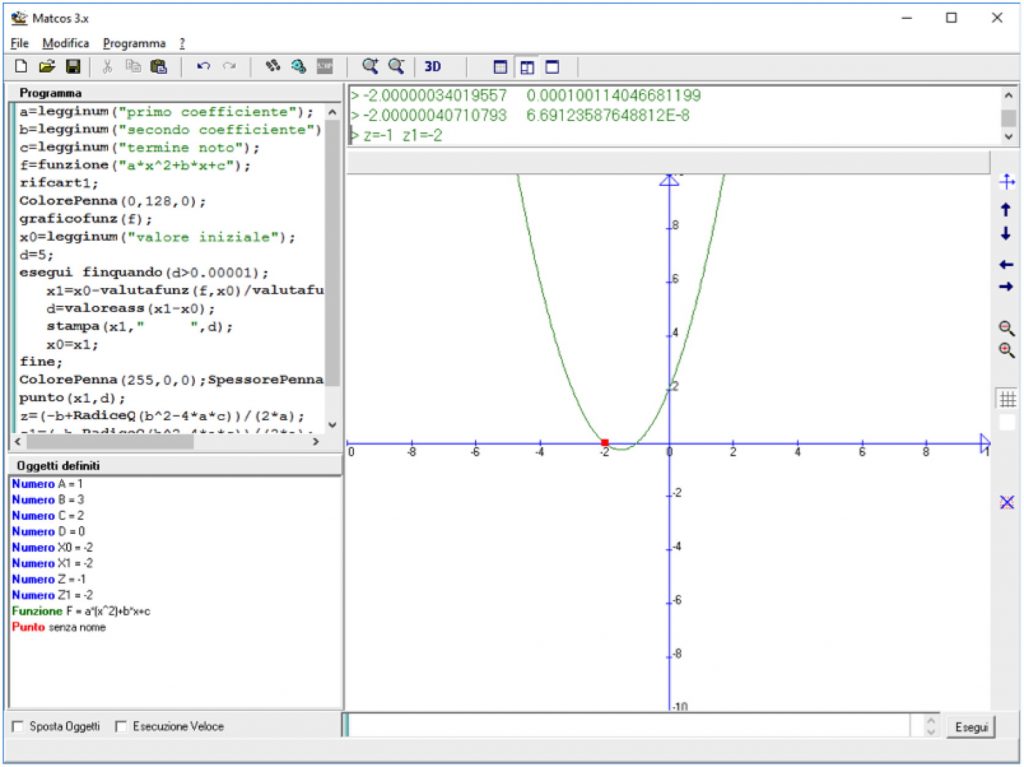
Radici di equazioni di secondo grado con il metodo di Newton
Come utile esercizio di Programmazione nell’ultimo anno della scuola superiore o comunque dopo aver acquisito i concetti matematici richiesti, si può proporre questo programma o una sua versione adeguata a particolari situazioni didattiche. Il programma presenta vari spunti didattici per approfondire e/o chiarire il concetto di approssimazione, ma anche il concetto di successione numerica e del relativo limite.
a=legginum(“primo coefficiente”);
b=legginum(“secondo coefficiente”);
c=legginum(“termine noto”);
f=funzione(“a*x^2+b*x+c”);
rifcart1;
ColorePenna(0,128,0);
graficofunz(f);
x0=legginum(“valore iniziale”);
d=5;
esegui finquando(d>0.00001);
x1=x0-valutafunz(f,x0)/valutafunz(derivatafunz(f),x0);
d=valoreass(x1-x0);
stampa(x1,” “,d);
x0=x1;
fine;
ColorePenna(255,0,0);SpessorePenna(3);
punto(x1,d);
z=(-b+RadiceQ(b^2-4*a*c))/(2*a);
z1=(-b-RadiceQ(b^2-4*a*c))/(2*a);
stampa(“z=”,z,” z1=”,z1);
Alla scoperta del concetto di limite
Il programma può essere illustrato nella sua logica agli allievi e poi eseguito, anche passo – passo, varie volte. Esso ha lo scopo di facilitare la comprensione di uno dei concetti più difficili e profondi dell’analisi matematica relativi alla scuola secondaria superiore. Infatti il concetto di limite difficilmente viene recepito nella sua essenza e la pratica didattica si limita, nella maggior parte dei casi, all’acquisizione di qualche tecnica ripetitiva per il calcolo di semplici limiti di successioni o funzioni. In qualche caso si tenta di imparare a “memoria” la classica definizione
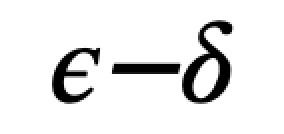
L’uso del programma, attraverso la tabulazione, può far intuire il concetto di limite e la profondità della definizione sopracitata.
Rifcart;
Stampa(“Il programma permette di studiare il comportamento di una funzione in un intorno simmetrico di un punto”);
f=leggifunz(“introdurre la funzione”);
xO=legginum(“punto limite”);
C=punto(xO,0);
Colore(8);
Stampa(“Per evidenziare lo studio della funzione di un intorno del punto si traccera’ il grafico della retta di equazione X=”, xO);
s=rettapar_asse(“y”,xO);
stampa(“Il grafico della retta verra’ cancellato dopo aver calcolato le coordinate dei punti della curva richiesti”);
n=10;
ms=matrice(n,2);
md=matrice(n,2);
h=1/n;
xs=xO-n*h;
xd=xO+n*h;
PER (i DA 1 A n) ESEGUI;
ys=valutafunz(f,xs);
ms(i,1)=xs;
ms(i,2)=ys;
Colore(4);
punto(xs,ys);
xs=xs+h;
yd=valutafunz(f,xd);
md(i,1)=xd;
md(i,2)=yd;
Colore(3);
punto(xd,yd);
xd=xd-h;
FINE;
cancella(s);
stampamatr(ms);
stampamatr(md);
stampa(“grafico della funzione nell’intorno del punto limite”);
colore(1);
graficofunz(f,xO-1,xO+1);
stampa(“grafico della funzione”);
graficofunz(f);
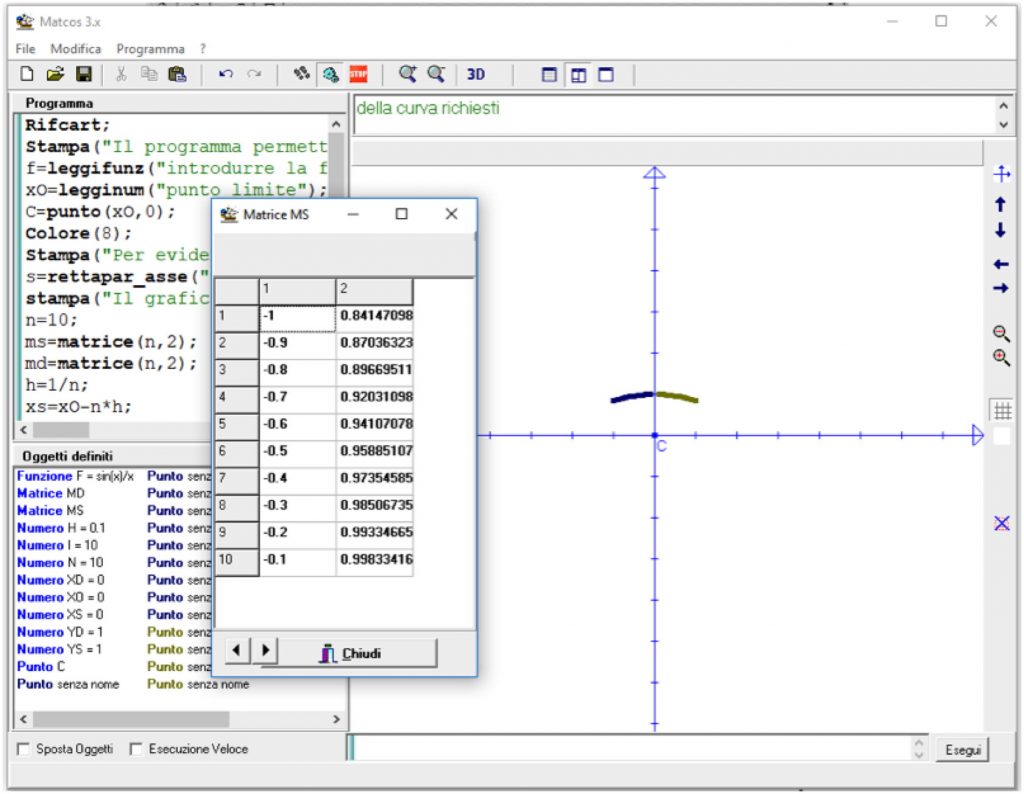
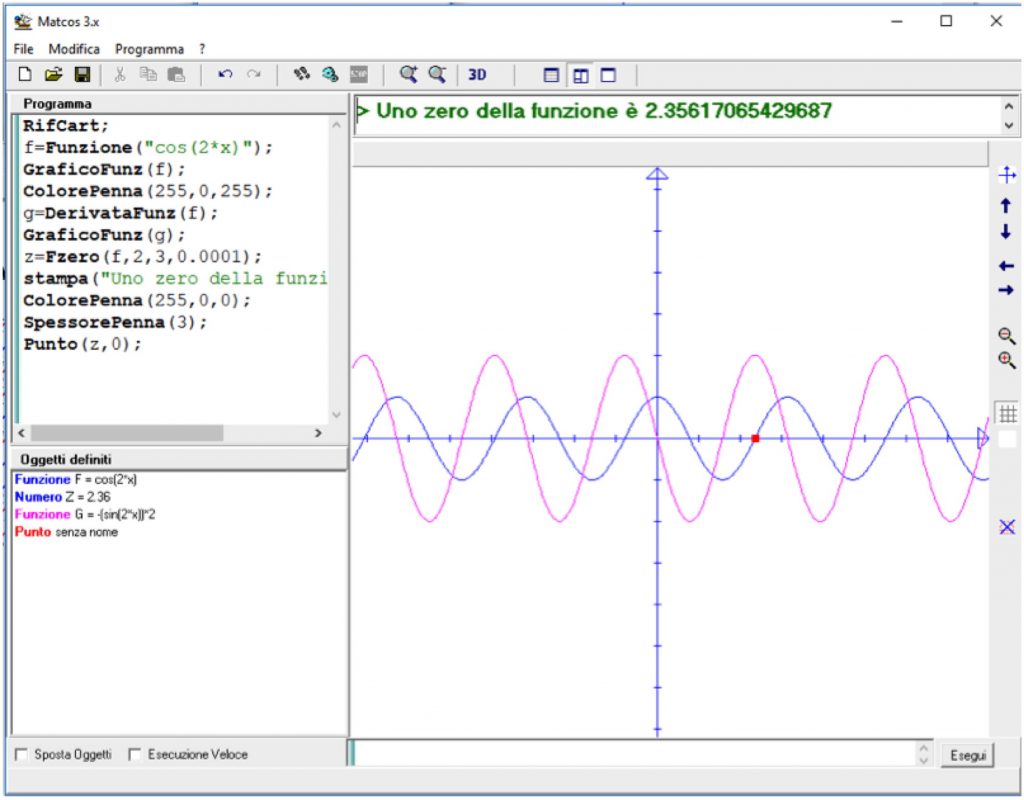
Alcune istruzioni per le funzioni
Il programma vuole solo mettere in risalto i comandi di cui il software dispone per lo studio delle funzioni. Naturalmente l’insegnante deve essere in grado di utilizzarle nel contesto didattico che creerà.
RifCart;
f=Funzione(“cos(2*x)”);
GraficoFunz(f);
ColorePenna(255,0,255);
g=DerivataFunz(f);
GraficoFunz(g);
z=Fzero(f,2,3,0.0001);
stampa(“Uno zero della funzione è “,z);
ColorePenna(255,0,0);
SpessorePenna(3);
Punto(z,0);
7. Conclusioni
In questo articolo abbiamo voluto sottolineare la necessità di un connubio didattico della Matematica e della Programmazione per il raggiungimento di un duplice fine formativo:
- apprendere la Matematica in modo attivo, rendendosi conto dei principali processi di pensiero e della costruzione logica della disciplina, anche nel contesto delle altre scienze;
- avviare al pensiero computazionale, o al Coding non come attività fine a se stessa (rischio naturale nella scuola secondaria e primaria, perché è difficile l’applicazione in concetti non scolastici), bensì come un’attività di pensiero che trova immediato supporto nella Matematica e nei suoi procedimenti algoritmici.
Ci rendiamo conto come tutto ciò sia non facile da realizzare, specialmente in assenza di strutture adeguate. L’esperienza condotta in aula e su un numero ragguardevole di classi [5-11] ha, però, incontrovertibilmente mostrato che è possibile raggiungere taluni livelli di comprensione, più che accettabili.
Concludiamo con l’auspicio che il Superiore Ministero continui a spronare questa “via didattica”, che soprattutto sappia “creare condizioni” che realmente rendano possibili i cambiamenti metodologici e didattici sperati.
Il software Matcos è disponibile gratuitamente in rete (http://lan.unical.it/costabile.php#software); eventuali chiarimenti e suggerimenti didattici possono essere richiesti al prof. Francesco Costabile: francesco.costabile@unical.it.
Eventuali materiali didattici e non disponibili in rete possono essere chiesti oltre che al prof. Costabile anche al dott. Tricoli: gianluca.tricoli@unical.it.
Bibliografia
[1] COSTABILE F.A. (a cura di)
Aspetti pedagogici e cognitivi dell’apprendimento della Matematica con le tecnologie. Carocci Editore Roma 2013.
[2] MOSCA G.
Coding, nelle scuole italiane è una materia inesistente,
https://w.w.w.wired.it/author/gmosca
[3] COSTABILE F.A., SERPE A.
Il progetto “Matematica e Computer”. Rassegna della istruzione, 2007, Vol. 1 Anno LXII.
[4] COSTABILE F.A.
Il Mondo delle figure. Pellegrini Editore (Cosenza) 2012.
[5] COSTABILE F.A.
Progetto Matematica per il terzo Millennio Edizioni Nuova Santelli (Cosenza) 2010 vol 1 e 2.
[6] COSTABILE F. A., SERPE A.
Progetto Pluriennale Matematica e Computer – Monitoraggio delle attività Modulo MatCos 2.1 – Anno Scolastico 2003 – 04. Vol. 986. Costabile F. A., Serpe A. (a cura di), Cap. 2, “L’insegnamento-apprendimento della Matematica nell’era del computer, S. Prospero s/S (MO): Centro Programmazione Editoriale. 2005. pp. 21-29.
[7] COSTABILE F. A., SERPE A.
Matematica & Computer. Progetto Pluriennale. Monitoraggio del Modulo MATCOS 2.2. Anno Scolastico 2004-2005, Quaderni di didattica Numero tematico, Luigi Pellegrini Editore, Cosenza, pp. 89-102.
[8] COSTABILE F. A.
Il Progetto Matematica e Computer, Atti del convegno Progetto “Matematica e Computer” – Giornata di lavoro con gli studenti protagonisti, Rende, Università della Calabria, 19 novembre, 2006, A cura di Costabile F. A., Serpe A., Luigi Pellegrini Editore, Cosenza, 2006, pp. 13-26.
[9] COSTABILE F. A., SERPE A.
Il Progetto “Matematica e Computer”: sinossi degli obiettivi e dei presupposti metodologici. Atti del convegno ATTI II Convegno Nazionale Matematica e Computer Giornata di lavoro con gli studenti protagonisti, Rende, Università della Calabria, 23 novembre, 2007, Pellegrini Editore Cosenza, 2007, Vol. 5, pp. 11-15.
[10] COSTABILE F. A., SERPE A.
MATEMATICA E COMPUTER III Ciclo di sperimentazione nella scuola media – Moduli MatCos 2.1 – 2.2 – 2.3 – Monitoraggio dei risultati – anni scolastici 2004/05 – 2005/06 -2006/07, 2007, Rapporto interno vol. 50. Progetto di riferimento: C.I.R.D.
[11] COSTABILE F. A., SERPE A.
MATEMATICA e COMPUTER III Ciclo di Sperimentazione Biennio Scuola Superiore – Moduli MatCos 2.4 – 2.5 – Monitoraggio dei risultati anni scolastici 2005/06 – 2006/07, 2007, Rapporto interno vol. 52. Progetto di riferimento: C.I.R.D.
[12] COSTABILE F. A., SERPE A.
MATEMATICA e COMPUTER II Ciclo di Sperimentazione Triennio Scuola Superiore – Moduli MatCos 2.6 – 2.7 – 2.8 – Monitoraggio dei risultati – anni scolastici 2004/05 – 2005/06 – 2006/07, 2007, Rapporto interno vol. 53. Progetto di riferimento: C.I.R.D.
